¿Cómo funciona una hipoteca?
Introducción
Hace poco tuve que buscar hipoteca y me sorprendió lo complicado que puede llegar a ser. Si bien existen un gran número de artículos que explican el funcionamiento técnico y todos los detalles financieros, lo que yo buscaba era una explicación sencilla del funcionamiento de una hipoteca o dicho de otro modo, cuánto dinero ganará el banco a mi costa y cómo. Mi razonamiento es simple, el banco no es ni nunca será tu amigo, así que es mejor que sepas lo que estás firmando con ellos porque puede ser una de las decisiones más importantes de tu vida.
Una de las primeras cosas que lees cuando te pones a investigar es que en España las hipotecas se calculan con el denominado sistema Frances. La fórmula de cálculo se puede ver aquí, pero es poco probable que entendamos lo que quiere decir si no tenemos conocimientos financieros previos. Por si eso fuera poco, a la ensalada hay que añadirle varios conceptos como el TIN o el TAE, si el tipo de interés es fijo o variable o el Euribor, vamos lio total.
Einstein decía que si no puedes explicar algo de forma simple no lo entienes lo suficiente, así que eso es lo que voy a intentar hacer a partir de este punto, escribir el árticulo que me habría gustado encontrar hace unas semanas.
El Sistema Francés
También denominado préstamo francés o sistema de amortización francés es el sistema de referencia que se usa en diversos países, España entre ellos. La fórmula de cálculo es todo menos trvival y auna el capital (el dinero que le debemos al banco), el tipo de interés (lo que vamos a pagar de más) y el tiempo (como número de cuotas). El principio básico es simple, todo lo que crezca en esa ecuación va a ser malo para el consumidor o hipotecado.
Para que nos hagamos una idea de lo que la fórmula calcula voy a separar los conceptos y explicarlos uno por uno.
Capital: Es el dinero que le debemos al banco sin intereses ni ningún otro tipo de recargo. Al principio será igual al importe que pedimos prestado pero se va a ir reduciendo con cada cuota pagada. Ahora bien no siempre se reducirá lo mismo y esta es la variable más interesante para el consumidor como explicaré más adelante.
Interés: Cuánto vamos a dar de más al banco por lo que nos han prestado. Aquí vamos a encontrar diversos términos como TIN o TAE pero los explicaré más adelante para no complicar las cosas de momento. El concepto de interés propiamente dicho debería ser muy sencillo, veamos un ejemplo con cálculo anual y cuotas mensuales que es lo normal. Imaginemos que nos prestan 120€ y el tipo es el 10% (sí, ya sé que es mucho). Al cabo de un año tendremos que devolver 120 + 10% = 120 + 12 = 132. Es decir que cada mes devolveríamos 11€ donde podríamos decir que 10€ provienen de lo que el banco nos prestó y 1€ es el beneficio del banco. Por ahora la cosa es sencilla, pero se complica algo con los dos siguientes factores.
Tiempo o número de cuotas: Por lo general el tiempo se va a medir en plazos o cuotas y como pagamos una vez se corresponderá con el número de mensualidades del préstamo. Digamos que en el ejemplo anterior, en lugar de pagar los 120€ en un año queremos hacerlo en dos con el mismo interes anual al 10%. Podríamos repetir el cálculo anterior y decir algo como 120/24 = 5. Cada mes pagaríamos 5€ de capital más 1€ de intereses. Hasta aquí todo parece correcto, pero hay un matiz muy interesante que juega a nuestro favor. Nuestra deuda con el banco se va reduciendo ¿No deberíamos reducir los intereses que genera esta deuda también? ¡Claro que sí! Dicho de otro modo, no tenenos por qué pagar los mismos intereses el día uno del préstamo cuando debemos 120€ que pasados 23 meses cuando solo debemos al banco 5€. Pero tengamos un poco de paciencia porque más adelante aclaro como se hace esto.
Cuota: Lo que vamos a pagar al banco. Hay que saber al menos dos cosas sobre ella. Lo primero es que la cuota permanece constante. Esto no es del todo cierto, porque cuando los intereses cambian la cuota se recalcula, pero la fórmula que calcula la cuota obtiene un valor constante, cosa distinta es que las condiciones de cálculo cambien, por ejemplo si sube el Euribor y la hipoteca es variable. En cambio en una hipoteca fija tendríamos justo este caso, las condiciones no cambian y por tanto la fórmula nos va a dar el valor de la cuota de forma precisa. Lo segundo que hay que saber es que cada cuota tiene dos partes. Aunque la cuota sea la misma todo el tiempo esas dos partes siempre cambian. Igual el punto anterior te ha dado una pista sobre esto, las dos partes son el capital y los intereses. Como con cada cuota que pagamos el capital que debemos al banco es menor, los intereses que ese capital genera a favor del banco van a verse reducidos en la siguiente cuota. Es justo lo contrario que ocurre cuando ponemos dinero en un depósito. El banco nos pagará intereses cada mes, cuanto más dinero añadimos al depósito, más recibimos. Con la hipoteca ocurre lo mismo, solo que genera intereses a favor del banco, cuanto más dinero debemos, más pagamos.
Show me the Money
Rod Tidwell (el personaje interpretado por Cuba Gooding Jr. en Jerry Maguire) era un tío con bastante sentido común, déjate de historias y enséñame el dinero. Las siguientes gráficas muestran lo explicado anteriormente de forma visual. Como en el caso anterior, los ejemplos no pretenden ser realistas sino ilustrativos. Aplican una fórmula de forma práctica para comprobar su funcionamiento, es un truco de mal estudiante que me salvó más de un examen.
Voy a usar como ejemplo un préstamo de 120.000€ en el que iré modificando los parámetros de interés y años de amortización para ver lo que ocurre. Tal y como mencionaba estos ejemplos no serán siempre realistas, pero sí interesantes. Del mismo modo los ejemplos tampoco reflejan otros gastos que existen en la práctica (comisiones, impuestos, etc.), nos centramos en el puro coste del préstamo que nos aplicará el banco dependiendo del tipo de interés.
EJEMPLO 1
Importe: 120.000 €
Interes: 0%
Plazo: 0 Años
Aquí no hay mucho que explicar, el dinero se devuelve de forma inmediata, no nos iba a resultas muy útil, ya que no podríamos usarlo para nada.
EJEMPLO 2
Importe: 120.000
Interes: 0%
Plazo: 1 Año
Aquí el banco nos presta el dinero sin cobrarnos nada a cambio, con lo que la cuota sería igual al capital dividido por el número de plazos. No pagamos nada de intereses, pero es muy probable que nos sea imposible asumir una cuota de 10.000€ mensuales, así que en el siguiente ejemplo vamos a aumentar el número de años.
EJEMPLO 3
Importe: 120.000
Interes: 0%
Plazo: 10 o 20 años
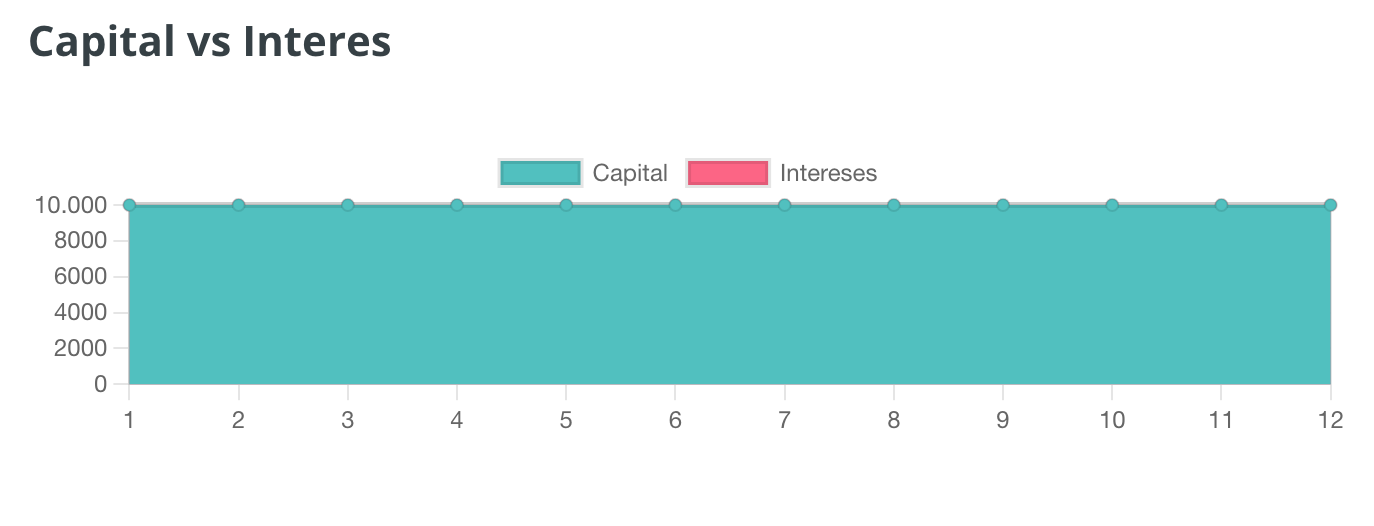
Aquí tendríamos 120 cuotas en 10 años y el banco seguiría actuando como una ONG, prestándonos dinero sin ganar nada a cambio. La cuota es fácil, 1000€ al mes. Si multiplicamos por dos el tiempo pagaríamos la mitad cada mes, así que con 20 años la cuota sería de 500€. Recordemos que esto es tan sencillo por la ausencia de intereses, vamos a ver lo que ocurre cuando los añadimos.
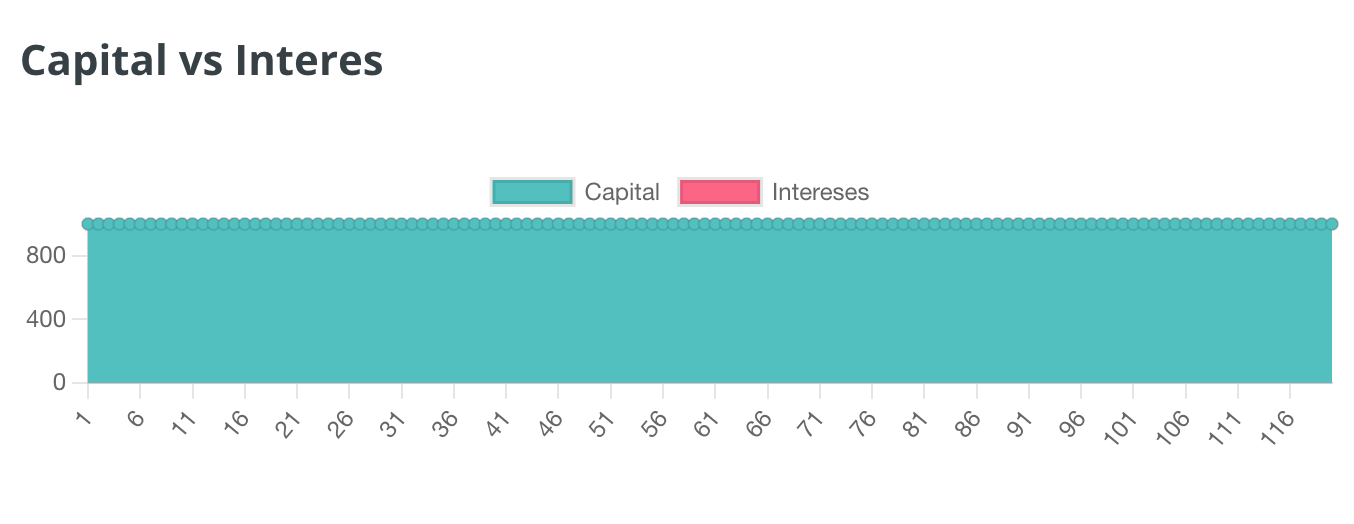
EJEMPLO 4
Importe: 120.000
Interes: 1%
Plazo: 20 años
Aquí introducimos intereses y la cosa comienza a ponerse “interesante”. El 1% es un interes bajo, así que en nuestra primera cuota solo tendríamos que dedicar 100€ a pagar el interes producido por los 120.000€ -> 120.000 / 100 x 1 = 1200 (anual) -> 1200 / 12 meses = 100€ (al mes). Como el capital se distribuye según la fórmula en el número de años, pagaremos 451.87€ de nuestra deuda, sobre una cuota total de 551,87€. En resumen, casi todo nuestro dinero se está dedicando a reducir nuestra deuda con el banco. En concreto un 81.88% de esa cuota va a reducir el préstamo. Si sumamos todos los intereses del mismo, al final del préstamo le habremos dado al banco 12449,56€ extras, que podríamos decir que es lo que nos ha costado el préstamo.
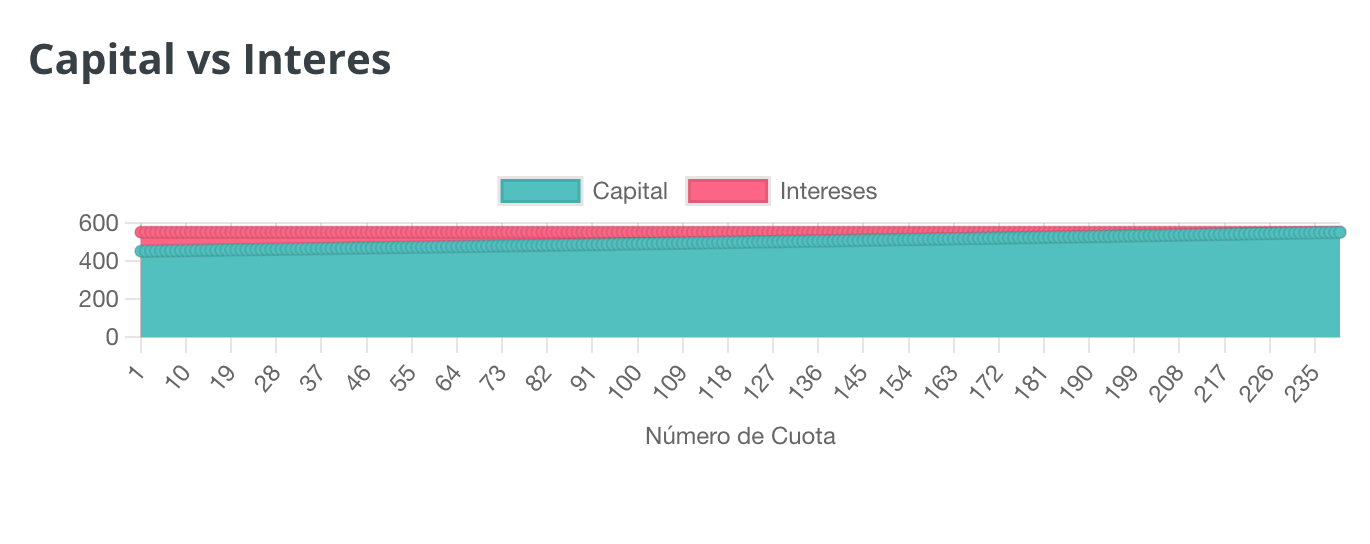
¿Qué pasa si sube el interés?
EJEMPLO 5
Importe: 120.000
Interes: 3%
Plazo: 20 años
Aquí es cuando comienzan las tiranteces. Si miramos de nuevo la primera cuota que es la más sencilla de analizar, vemos que ahora nos cuesta 665,52€ de los que 300€ serán de intereses, el triple que antes. El capital reducido por la cuota será de 365,52€, solo un 54,92% de nuestro dinero se dedica a reducir lo que debemos y por tanto los intereses que eso genera. Esto se traduce en el que el costo total del préstamo es de 39724,11€, más del triple que antes. Pero aquí se puede producir un efecto indeseado, ¿qué pasa si con la subida de intereses hemos obtenido una cuota mayor de la que queremos pagar? En este punto solo nos quedará jugar con el tiempo y aumentar el número de cuotas para pagar menos en cada una, vamos a probar esto.
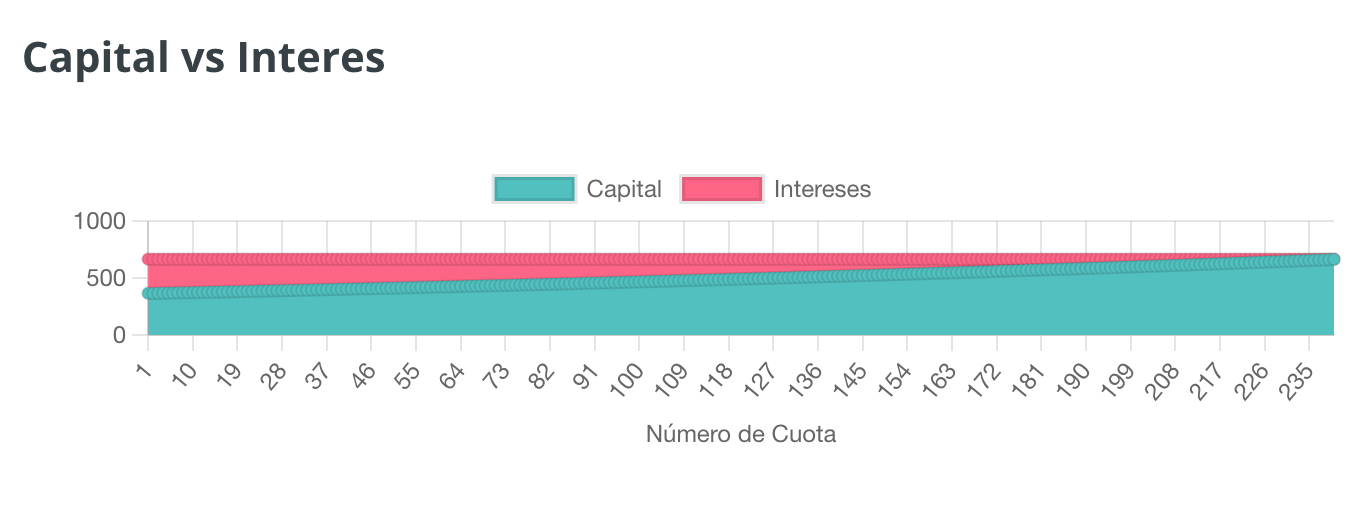
EJEMPLO 6
Importe: 120.000
Interes: 3%
Plazo: 30 años
Aquí estamos rebajando la cuota bastante, nuestra primera cuota sería de 505,92€, sin embargo el 3% sigue siendo de 300€ y como consecuencia casi todo nuestro dinero se va en pagar intereses. Concretamente solo 205,92€ (un 40,70% de la cuota) de nuestro dinero se va a dedicar a reducir nuestra deuda con el banco. Podríamos decir que es la muerte a pellizcos, ya que el coste total del préstamo será de 53816,43€ en este caso.
También podemos ver en la gráfica de cuota vs. intereses que la parte roja del préstamo (los intereses) ha crecido de forma alarmante.
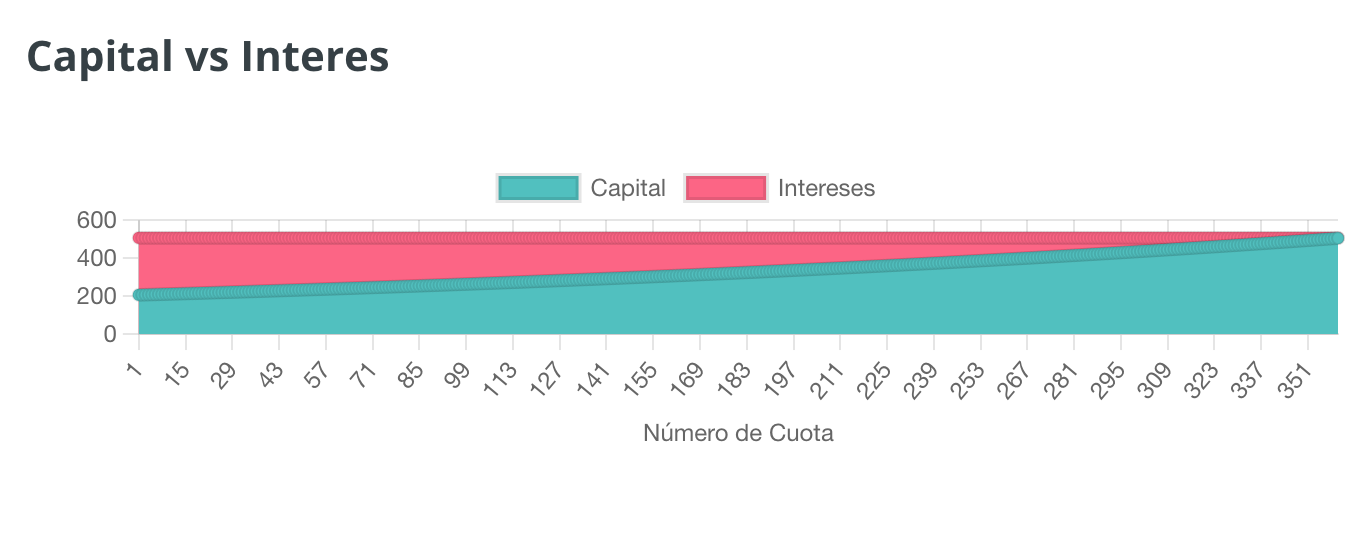
EJEMPLO 7
Importe: 120.000
Interes: 5%
Plazo: 30 años
¿Y si los tipos suben aún más? Imaginemos que en este último escenario los tipos suben al 5%. Nuestra gráfica se vuelve bastante espantosa ya que el primer mes del préstamo producirá 500€ de intereses. Con una cuota de 644,19€, la parte de nuestro dinero que se dedica a “resolver nuestro problema” es mínima, mientras que la que hace rico al banco es considerable. Por supuesto el coste del préstamo se dispara: 95339,35€.
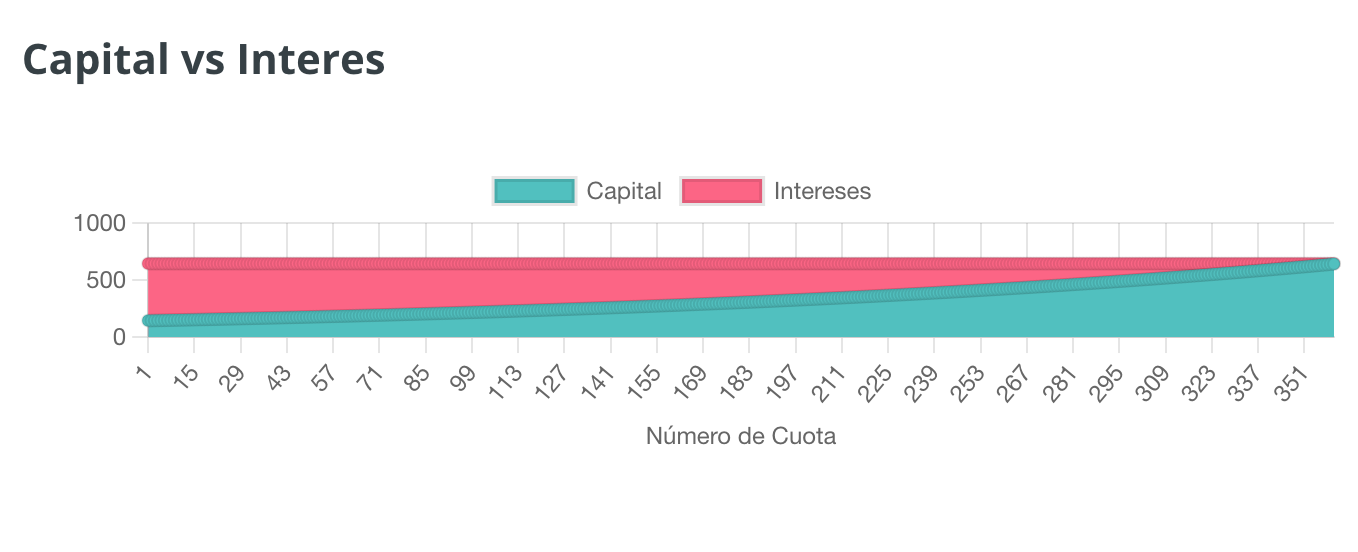
Pero ¿qué conclusiones útiles podemos sacar de todo esto?
La primera es que el interés nos hace más daño cuanto más temprano sea el estadio en el que se encuentre nuestro préstamo. En los ejemplos anteriores el tipo se presenta como un valor fijo, pero sabemos que las hipotecas variables están sujetas a las subidas y bajadas de los tipos de interés. Utilizando nuestro ejemplo al 1%, si nos sube al 5% el último año, donde nos quedan unos 7000€ que devolver al banco, los intereses producidos serán de 29€ al mes, lo que no nos va a incrementar demasiado la cuota, aunque los intereses se hayan multiplicado por 5.
La segunda es que el tiempo es un arma de doble filo. Si bien nos ayuda a pagar más comodamente, hace que le demos al banco dinero de forma sostenida durante más tiempo. Es por esto que los bancos intentaran alargar el préstamo siempre que puedan.
¿Deberíamos por tanto acortar el préstamo?
Las matemáticas dirían que sí, pero obviamente tenemos que poder pagarlo. Por eso debemos tener en cuenta ambos factores y ser conscientes de que alargar la deuda no sale gratis.
Otro factor a considerar es que cambiar las condiciones del préstamo no es nada sencillo, con lo que debemos ser cautelosos intentando acortar demasiado los plazos para ahorrar dinero.
¿Hay algo que pueda hacer entonces?
Una buena alternativa puede ser tratar de reducir el capital del préstamo lo antes posible si disponemos de un dinero extra. Cuanto antes hagamos esto antes reduciremos la cantidad que genera intereses a favor del banco. También hay que comprobar si esto tiene una penalización, esto suele depender del tipo de préstamo y por lo general no ocurre para préstamos de tipo variable. Es además un factor que se puede negociar con el banco a la hora de concedernos el préstamo.
¿Entonces qué tipo de hipoteca elijo?
Esta es la pregunta del millón y para poder responderla con seguridad necesitaríamos una bola de cristal, o dicho de otro modo, necesitaríamos saber si los tipos van a subir o bajar. Vamos a hacer un resumen rápido de los pro y contras de cada tipo.
Hipoteca Fija: Es la más simple de entender y todos los ejemplos anteriores usan un tipo fijo. Aquí pactamos un tipo de interes con el banco que se mantendrá durante toda la vida útil del préstamo. Como el banco no va a poder cambiarlo cuando nos oferta una hipoteca siempre va a utilizar un valor que estará por encima de lo que en ese momento será el precio del dinero al que prestarían de forma variable. De ese modo, si el Euribor sube, es bastante probable que salgamos beneficiados, mientras que si baja, las condiciones iniciales, que ya de por si son algo desfavorables en ese momento, pasarán a ser peores. Se puede decir que aquí estamos comprando tranquilidad. Cabe señalar que en este tipo de hipoteca la amortización (devolución anticipada) de capital suele tener una penalización.
Hipoteca Variable: Era la clásica hasta que los tipos comenzaron a subir. Si el Euribor sube pagas más, si baja menos. Como vimos anteriormente, el “daño” que nos va a hacer la subida de intereses dependerá del capital que nos quede por pagar. Una subida importante de tipos en el primer año no es lo mismo que en el último. Tomando como referencia los ejemplos 4 y 5 anteriores, si pedimos 120.000€ a 20 años y el Euribor sube del 1% al 3%, la primera cuota pasaría de 551€ a 665€, mientras que si ocurre transcurridos 15 años cuando solo nos quedan 32.000€ por amortizar, la cuota subiría a 589,65€. Las hipotecas variables no suelen tener penalización por amortización anticipada, con lo que aplicaría lo que antes decíamos, cuanto antes reduzcamos el capital, más ahorraremos. Volviendo al ejemplo 5, en la cuota 200 deberíamos al banco 25983,63€, si los pagamos en ese momento ahorraríamos 1362,60€, mientras que si los tuvieramos inicialmente, es decir, pidieramos alrededor de 94400€, el costo del préstamo bajaría 8574,99€.
Hipoteca Mixta: Aquí tenemos una mezcla ya que la hipoteca se comporta como fija un número de años y pasa a variable despues. Puede ser una opción interesante cuando los tipos pueden subir por dos razones. La primera es la obvia, el tipo fijo nos proteje frente a la subida del Euribor. La segunda es la que se explica anteriormente, si llegamos al tipo variable y los tipos han subido, nuestro capital se habrá reducido, con lo que el impacto en ese punto será menor. Logicamente todo esto solo es favorable si los tipos suben, si bajan habremos perdido dinero durante la parte fija. Es bueno leer todas las condiciones ya que en este tipo de hipoteca las partes fijas y variables suelen ser distintas. Por si esto fuera poco complicado también es fácil que podamos jugar con el número de años fijos o variables.
¿Hay algo más?
Si claro, si no teníamos bastante con todo lo anterior hay unos cuantos factores más que merece la pena conocer. Uno bastante obvio es que los bancos venden los préstamos hipotecarios junto con otros productos que bonifican las hipotecas. Hablamos de seguros de vida, hogar, cuentas nómina, planes de pensiones y similares. Como es lógico estamos adquiriendo un producto, con lo que eso aporta cierto valor a la operación. Por ejemplo, es fácil que queramos un seguro para nuestro hogar y si este nos bonifica la hipoteca, pues tanto mejor, pero ¿es más caro que el de la competencia? ¿nos compensa la bonificación la diferencia de precio? En algunos casos esto puede tener algo de truco, por ejemplo, si bien el seguro de vida aporta un valor obvio, es posible que su coste se vea incrementado más de lo que esperamos conforme pasan los años y nuestra edad sube.
Todos estos costes más o menos ocultos y otros que no corresponden a productos adicionales, como la comisión de apertura si la hubiera, vienen recogidos en un factor que se denomina TAE y es un porcentaje que debería servirnos para comparar distintas hipotecas en igualdad de condiciones. Es recomendable tener cierto cuidado a la hora de interpretarlo porque algunas entidades pueden no tener el mismo rigor que otras a la hora de calcularlo, sobre todo si hay factores que no están totalmente definidos, como las potenticiales bonificaciones.
Un ultimo detalle que es interesante es que el valor que hemos venido utilizando hasta ahora en los ejemplos anteriores es el TIN, que es el interés o precio al que el banco nos vende el dinero, mientras que el TAE incluye eso más el resto de costes que asumimos con la hipoteca.
